⏱시계열 분석(time series analysis)
- 시계열(시간의 흐름에 따라 기록된 것) 자료(data)를 분석하고 여러 변수들간의 인과관계를 분석
1. 시계열 데이터
- 시계열 데이터는 시간을 기준으로 관측된 데이터
- 보통 일 → 주 → 월 → 분기 → 년 또는 Hour 등 시간의 경과에 따라 관측
ex) GDP, 주가, 거래액, 매출액, 승인금액 등을 시간에 흐름에 따라 정의한 데이터
1) 연속시계열
- 자료가 연속적으로 생성
- 대부분의 데이터 형태가 연속형이나 이산형 정의하여 분석
2) 이산형 시계열
- 일정 시차(간격)를 두고 관측되는 형태의 데이터
- 대부분 이산형 데이터를 분석
2. 시계열 데이터의 목적
- 예측 : 금융시장 예측, 수요 예측등 미래의 특정 시점에 대한 관심의 대상(반응변수)을 예측
- 시계열 특성 파악 : 경향(Trend), 주기, 계절성, 변동성(패턴) 등 관측치의 시계열 특성 파악
* 전통적인 시계열 분석방법
- 이동 평균 모형(moving average) : 최근 데이터의 평균을 예측치로 사용
- 자기 상관 모형(Autocorrelation) : 변수의 과거 값의 선형 조합을 이용하여 예측하는 방법
- ARIMA(Autoregressive Integrated Moving Average) : 관측값과 오차를 사용해서 모형을 만들어서 미래를 예측
- 지수평활법 : 현재에 가까운 시점에 가장 많은 가중치 주고 멀어질수록 낮은 가중치를 주어서 미래를 예측
3. 시계열 요소
1) 경향/추세(trend)
- 시계열 데이터가 장기적으로 증가(감소)할 때, 추세가 존재함
1) 계절성(seasonality)
- 특정 기간(1년마다), 어떤 특정한 때나 1주일마다 특정 요일에 나타나는 것 같은 계절성 요인
ex)패션업종 매출, 요일별 온라인 쇼핑몰 매출 등
3) 주기성(cycle)
- 일정한 주기(진폭)마다 유사한 변동이 반복되는 현상
- 보통 경기 순환(business cycle)과 관련이 있으며 지속기간은 2년
ex) 주가 업종별 개별(업종) 주가
4) 불규칙요인(Irregular movements)
- 예측하거나 제어할 수 없는 요소
ex) 회귀분석의 오차와 같은 항목
4. 시계열 분석 방법
1) 단기예측
- 수학적 이론에 의존하고 시간에 따른 변동이 많은(빠른) 시계열 자료에 적용
- 지수평활법, 시계열 해법, Box-jenkins 방법
2) 장기예측
- 장기적으로 예측이 필요한 데이터
- 회귀분석 방법론
3) 직관적 방법
- 시간에 따른 변동이 느린 데이터에 활용
- 지수평활법, 시계열분해
4) 다중 시계열
- 시계열데이터와 설명변수가 있는 경우
- 회귀분석(계량경제)방법, 전이함수모형, 다변량 ARIMA
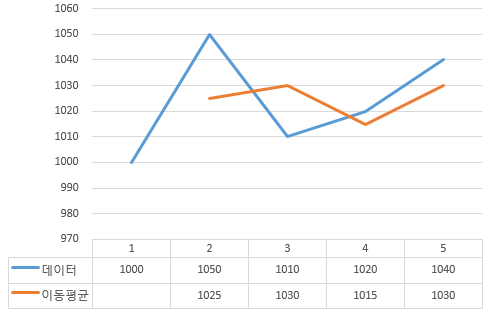
5. 이동평균법
- 최근 데이터의 평균을 예측치로 사용
- 단순 이동 평균 :
6. 지수평활법
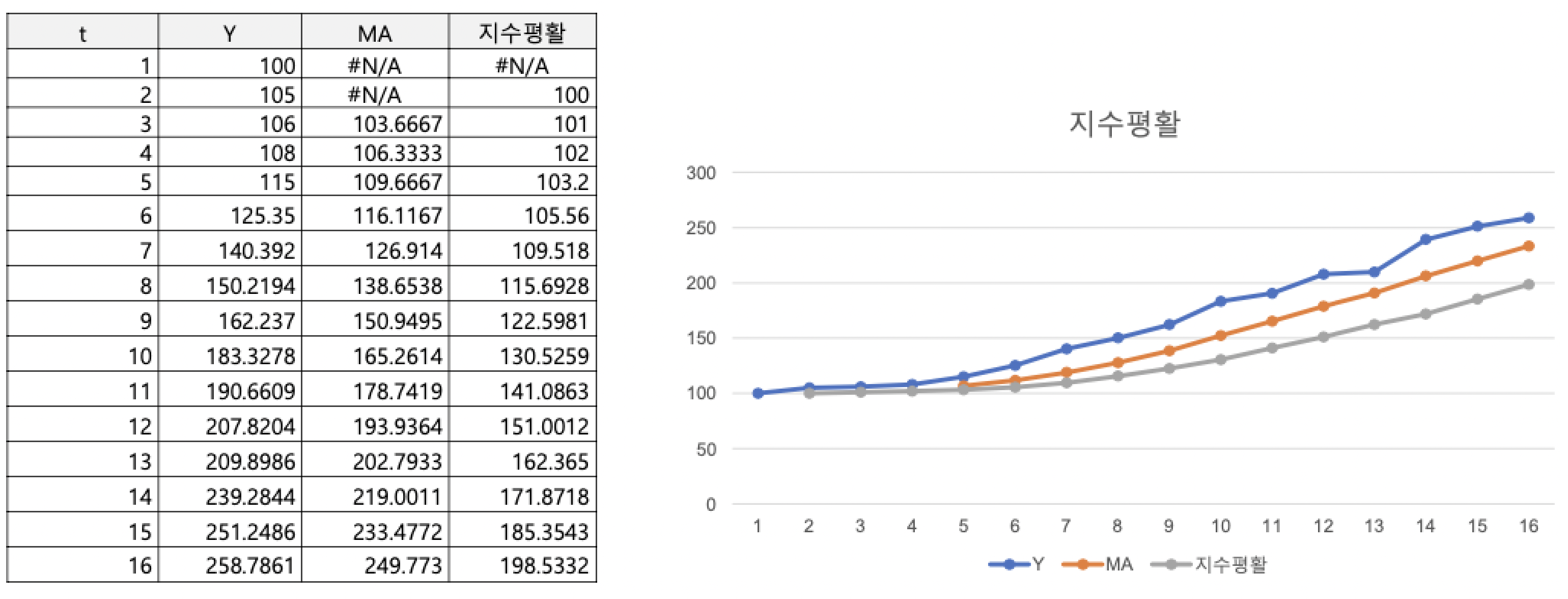
- 현재에 가까운 시점에 가장 많은 가중치 주고 멀어질수록 낮은 가중치를 주어서 미래를 예측
- 모든 관측값을 이용하면서 예측하는 시점에 가까울수록 비중을 두어 최근값이 예측시 더 많은 기여를 하도록 만드는 방법
,
(는 지수평활계수)
'통계 & 수학 > 통계학' 카테고리의 다른 글
| [통계] 분산 분석 (0) | 2022.05.19 |
|---|---|
| [통계] 다중 회귀분석 (0) | 2022.05.19 |
| [통계] 단순 회귀분석 (0) | 2022.05.19 |
| [통계] 상관분석 (0) | 2022.05.19 |
| [통계] 범주형 자료 분석 (0) | 2022.05.18 |
![[통계] 시계열 분석](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FclFUAH%2FbtrCyZv6lDR%2FKxXixkveMJ7WHPqNG01ERk%2Fimg.png)