🔍 확률
- 모든 경우의 수에 대한 특정 사건이 발생하는 비율
1. 표본 공간(Sample Space)
- 표본 공간이란 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
- 동전 던지기의 경우 S = {앞면, 뒷면} , 주사위던지기 S = {1,2,3,4,5,6}
- P(A) = A/S P(A) : 사건 A가 일어날 확률 / (S) : 표본 공간
2. 통계적 확률 정의
1) 상대도수
- 어떤 시행을 N번 반복했을 때, 사건 A에 해당하는 결과가 r번 일어난 경우 r/N
2) 통계적 확률(경험적 확률)
- N이 무한히 커지면 상대도수는 일정한수로 수렴
$\lim\frac{r}{N} $
3. 확률의 성질
1) 합사건(union) : 사건 A 또는 사건 B가 일어날 확률
2) 곱사건(intersection) : 사건 A와 사건B가 동시에 일어날 확률
3) 여사건(complement) : 사건A가 일어나지 않을 확률
4) 배반사건(mutually exclusive event) : 사건 A와 사건B가 동시에 일어 날 수 없는 확률

🗝 조합과 순열
1. 팩토리얼(Factorial : !)
- n개를 일렬로 늘여 놓은 경우의 수를 n!로 표현
$n! = 1\cdot2\cdot3\cdot\cdot\cdot\cdot n$
$0! = 1$
2. 순열(Permutation)
- 순서를 고려하여 n개 중 r개를 뽑아서 배열하는 경우의 수
$_{n}\mathrm{P}_{r}= \frac{n!}{(n-r)!}$
(단, $0 <r \leq n$)
[모듈] 순열(permutation)
🔍 문제 순열을 생성하는 모듈을 만들어 값을 구한다. 🗝 사용함수 nPr : n!/(n-r)! from itertools import permutations. : itertools 패키지에 저장된 permutations(순열) 모듈 사용 permutations([a], b) :..
designingdata.tistory.com
3. 조합(Combination)
- 순서를 고려하지 않고 n개중 r개를 뽑아서 배열하는 경우의 수
$_{n}\mathrm{C}_{r}= \frac{_{n}\mathrm{P}_{r}}{r!} = \frac{n!}{r!(n-r)!}$
(단, $0 <r \leq n$)
[모듈] 조합(combination)
🔍 문제 모듈을 사용하여 조합 출력 🗝 사용함수 nCr : nPr/r! = n!/(n-r)! from itertools import combinations. : itertools 패키지에 저장된 combinations(순열) 모듈 사용 combinations([a], b) : 리스..
designingdata.tistory.com
🎯 조건부 확률( conditional probability)
- 어떤 사건 A가 발생한 상황에서(주어졌을때) 또 하나의 사건 B가 발생할 확률

1. 확률의 곱셈 법칙

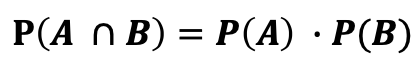
2. 베이즈 정리
- 함수 호출 시 함수에 데이터 전달 가능


'통계 & 수학 > 통계학' 카테고리의 다른 글
| [통계] 모집단과 표본 분포 (0) | 2022.05.18 |
|---|---|
| [통계] 확률분포 - 연속형 확률 분포 (0) | 2022.05.17 |
| [통계] 확률분포 - 이산형 확률분포 (0) | 2022.05.17 |
| [통계] 확률 변수 (0) | 2022.05.17 |
| [통계] 데이터의 이해 (0) | 2022.05.17 |
![[통계] 확률](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F7NLaq%2FbtrCkLS5lI8%2FALXPHjUHBesUsHPHWFDW3K%2Fimg.png)